机器学习:笔记 - Machine Learning Note

2. 模型评估与选择

2.1 经验误差与过拟合

在m个样本中有a个样本分类错误

错误率(Error rate): $E = \frac{a}{m}$
在训练集上的误差称训练误差(training error)或经验误差(empirical error)
在新样本上的误差称泛化误差(generalization error)
精度(Accuracy): $1 - E$
过拟合(Overfitting): 模型在训练数据上表现很好,但在测试数据上表现糟糕,这通常是因为模型过于复杂,以至于“记住”了训练数据的噪声.
过拟合(Overfitting): 模型在训练数据上表现很好,但在测试数据上表现糟糕,这通常是因为模型过于复杂,以至于“记住”了训练数据的噪声.

与NP的关系:
若可以彻底避免过拟合，则通过经验误差最小化就可以获最优解，这就意味着我们构造性的证明了P = NP

2.2 评估方法

2.2.1 留出法

留出法(Hold-out Method) 留出法通常将数据集分为训练集(S)和测试集(T)，有时还可以进一步将训练集分为训练集和验证集。在使用留出法时, 一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果

注意:
训练/测试集的划分要尽可能保持数据分布的一致性, 避免因数据划分过程引入额外的偏差而对最终结果产生影响, 例如在分类任务中至少要保持样本的类别比例相似
若令训练集S包含绝大多数样本, 则训练出的模型可能更接近于用D训练出的模型, 但由于T比较小，评估结果可能不够稳定准确; 若令测试集T多包含一些样本, 则训练集S与D差别更大了, 被评估的模型与用D训练出的模型相比可较大差别, 从而降低了评估结果的保真(fidelity)

2.2.2 交叉验证法

交叉验证法(cross validation/k-fold cross validation)先将数据集D划分为k个大小相似的互斥自己.

每个子集 $D_i$ 都尽可能保持数据分布的一致性, 即从D中通过分层采样得到.
每次用k-1个子集的并集作为训练集, 余下的那个子集作为测试集
这样就可获得k组训练/测试集, 从而可进行k次训练和测试, 最终返回的是这k个测试结果的均值.

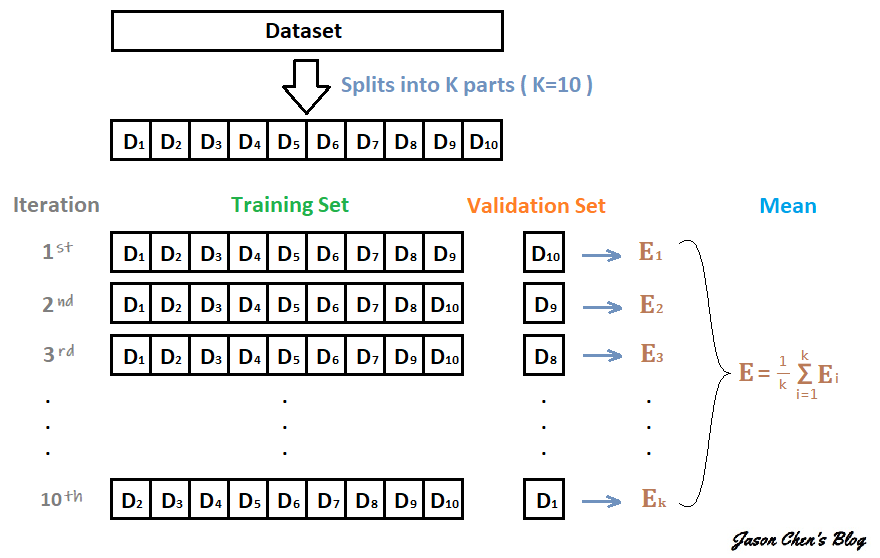
缺点: 测试样本数量大时计算开销极大

k最常用取值是10, 此时成为"10折交叉验证"
数据集D划分为k个子集同样存在多种划分方式, 为减小因样本划分不同而引入的差别, k折交叉验证通常要随机使用不同的划分重复p次, 最终的评估结果是这p次k折交叉验证结果的均值, 例如常见的有"10次10折交叉验证"

2.2.3 自助法

自助法(bootstrapping)在给定包含m个样本的数据集, 对其采样产生数据集D':

每次随即从D中挑选一个样本, 将其拷贝放入D
再将该样本放回初始数据集D中，使其仍有机会被再次采样
重复m次后，会获得包含m个样本的数据集D' > 样本适中不被采到的概率为 $(1-\frac{1}{m})^m$ , 取极限为 0.368
约有36.8%样本未出现在采样数据集D'中, 这时用D'作为训练集, D\D'用作测试集 > 这样的测试结果成为"包外估计"(out-of-bag estimate)

优点: 在数据集较小时, 难以有效的划分训练/测试集时很有用; 能从初始数据集中产生多个不同的训练集, 对集成学习有好处
缺点: 改变了初始数据集的分布, 可能引入估计偏差

2.2.4 调参和最终模型

在进行模型估计和选择时, 除了要对使用学习算法进行选择, 还需对算法参数进行设定, 这就是通常所说的"参数调节"/"调参"(parameter tuning)

2.3 性能度量

对学习器的泛化性能进行评估, 不仅需要有效可行的实验估计方法, 还需要有衡量模型泛化能力的评价标准，即性能度量(performance measure)

在预测任务中, 给定样例集 $D = \{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}$ , 其中 $y_i$ 是实例 $x_i$ 的真实标记. 要估计学习器 $f$ 的性能, 就要把学习器预测结果 $f(x)$ 与真实标记 $y$ 进行比较

均方误差(mean squared error):
$E(f;D) = \frac{1}{m}\sum\limits^m_{i=1}(f(x_i) - y_i)^2$
对于数据分布$D$和概率密度函数$p(·)$，均方误差可描述为:
$E(f;D) = \int_{x\thicksim D}(f(x)-y)^2p(x)dx$

2.3.1 错误率与精度

错误率定义为:

E(f;D) = \frac{1}{m}\sum\limits^m_{i=1}I(f(x_i)\neq y_i)

精度定义为:

acc(f;D) = \frac{1}{m}\sum\limits^m_{i=1}I(f(x_i) = y_i) = 1 - E(f;D)

更一般的，对于数据分布$D$和概率密度函数$p(·)$, 错误率和精度可分别表示为:
$E(f;D) = \int_{x\thicksim D}I(f(x_i)\neq y_i)p(x) dx$
$acc(f;D) = \int_{x\thicksim D}I(f(x_i) = y_i)p(x) dx = 1 - E(f;D)$

2.3.2 查准率、查全率与F1

真实情况	预测结果: 正例	预测结果: 反例
正例	TP	FN
反例	FP	TN

查准率(precision):

P = \frac{TP}{TP+FP}

查全率(recall):

R = \frac{TP}{TP + FN}

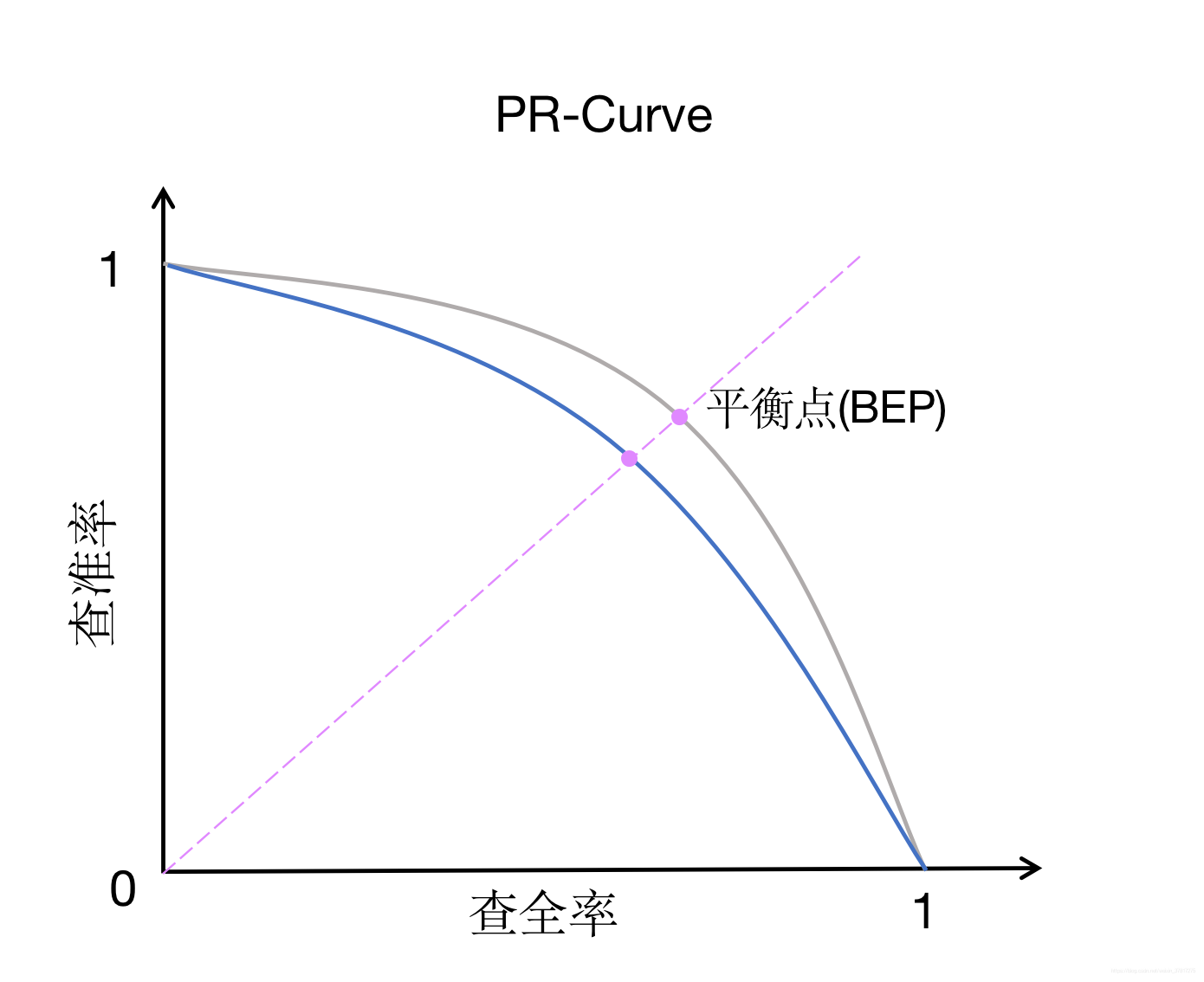
平衡点(Break-Even Point)是"查准率=查全率"时的取值。更常用的是F1度量:

F1 = \frac{2 \times P \times R}{P + R} = \frac{2 \times TP}{样例总数 + TP - TN}

$F_\beta$ 能够表达对查准率/查全率的不同的偏好, 定义为:

F_\beta = \frac{(1 + \beta^2) \times P \times R}{(\beta^2 \times P) + R}

$\beta > 1$ 时查全率有更大影响， $\beta < 1$ 时查准率有更大影响

多次训练:
现在个混淆矩阵上分别计算出查准率和查全率, 记为 $(P_1, R_1), (P_2, R_2),...,(P_n,R_n)$ , 再计算平均值, 这样就得到"宏查准率"(macro-P)、"宏查全率"(macro-R), 以及相应的"宏F1"(macro-F1):

macro-P = \frac{1}{n}\sum\limits^n_{i=1}P_i

macro-R = \frac{1}{n}\sum\limits^n_{i=1}R_i

macro-F1 = \frac{2 \times macro-P \times macro-R}{macro-P + macro-R}

也可先将各混淆矩阵的对应元素进行平均, 得到 $TP、FP、TN、FN$ 的平均值，分别记得 $\overline{TP}、\overline{FP}、\overline{TN}、\overline{FN}$ , 再基于这些平均值算出"微查准率"(micro-P)、"微查全率"(micro-R)和"微F1"(micro-F1):
$micro-P = \frac{\overline{TP}}{\overline{TP}+\overline{FP}}$
$micro-R = \frac{\overline{TP}}{\overline{TP}+\overline{FN}}$
$micro-F1 = \frac{2 \times micro-P \times micro-R}{micro-P + micro-R}$

2.3.3 ROC与AUC

ROC全称"受试者工作特征"(Receiver Operating Characteristic)曲线。ROC曲线的纵轴时"真正例率"(True Positive Rate, 简称TPR), 横轴是"假正例率"(Flase Positive Rate, 简称FPR), 定义为:

TPR = \frac{TP}{TP + FN}

FPR = \frac{FP}{TN + FP}

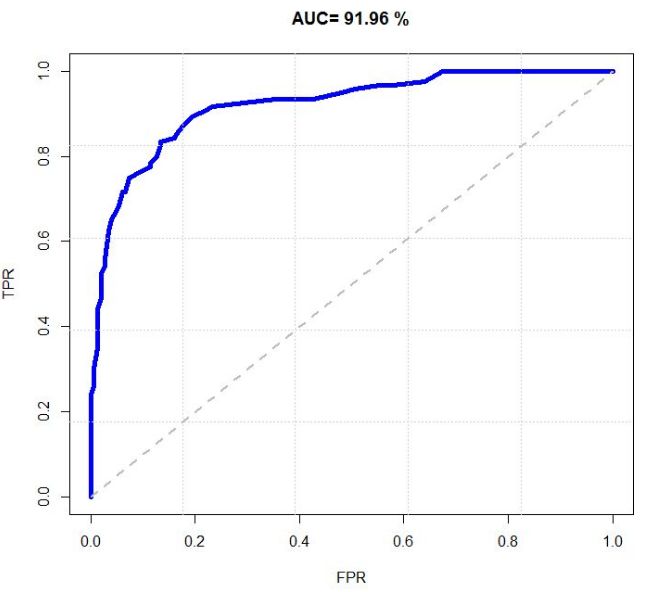
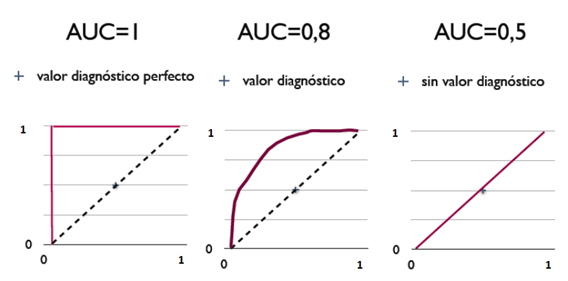
与P-R图类似，若一个学习器的ROC曲线被另一个学习器的曲线完全包裹, 则可以断言后者的性能优于前者.若两个学习器的ROC曲线发生交叉, 则难以一般性地断言两者孰优孰劣. 此时应比较ROC曲线下的面积, 即AUC(Area Under ROC Curve), 可估算为
$AUC = \frac{1}{2}\sum\limits^{m-1}_{i=1}(x_{i+1}-x_i)·(y_i+y_{i+1})$
AUC考虑的时样本预测的排序质量, 因此它与排序误差有紧密联系. 给定 $m^+$ 个正例和 $m^-$ 个反例, 令 $D^+$ 和 $D^-$ 分别表示正反例集合, 则排序损失(loss)定义为:
$l_{rank} = \frac{1}{m^+m^-}\sum\limits_{x^+\in D^+}\sum\limits_{x^-\in D^-}(I(f(x^+)<f(x^-))+\frac{1}{2}I(f(x^+)=f(x^-)))$
$AUC = 1 - l_{rank}$

2.3.4 代价敏感错误率与代价曲线

为权衡不同类型错误所造成的不同损失, 可谓错误赋予"非均等代价"(unequal cost)

真实类别	预测类别: 第0类	预测类别: 第1类
第0类	0	$cost_{01}$
第1类	$cost_{10}$	0

在非均等代价下，我们所希望的不再是简单的最小化错误次数, 而是希望最小化"总体代价"(total cost). "代价敏感"(cost-sensitive)错误率为:

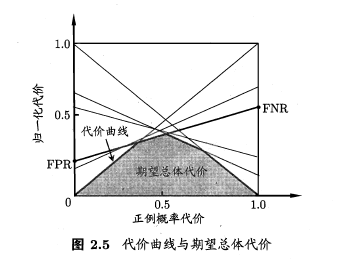
E(f;D;cost)=\frac{1}{m}(\sum\limits_{x_i\in D^+}I(f(x_i)\neq y_i) \times cost_{01}+ \sum\limits_{x_i\in D^-}I(f(x_i)\neq y_i) \times cost_{10})

在非均等代价下, ROC曲线不能直接反映出学习器的期望总体代价, 而"代价曲线"(cost curve)则可达到该目的. 代价曲线图的横轴时取值为[0,1]的正例概率代价:

P(+)cost = \frac{p \times cost_{01}}{p \times cost_{01} + (1 - p)\times cost_{10}}

其中 $p$ 是样例为正例的的概率, 纵轴是取值为[0,1]的归一化代价

cost_{norm} = \frac{FNR \times p \times cost_{01}+ FPR \times (1-p)\times cost_{10}}{p \times cost_{01} + (1-p)\times cost_{10}}

2.4 比较检验

2.4.1 假设验证(hypothesis test)

在包含m个样本的测试集上, 泛化错误率为 $\epsilon$ 的学习器被测得测试错误率为 $\hat{\epsilon}$ 的概率:

P(\hat{\epsilon};\epsilon) = \begin{pmatrix} m \\ \hat{\epsilon} \times m \end{pmatrix} \epsilon^{\hat{\epsilon} \times m}(1 - \epsilon)^{m - \hat{\epsilon} \times m}

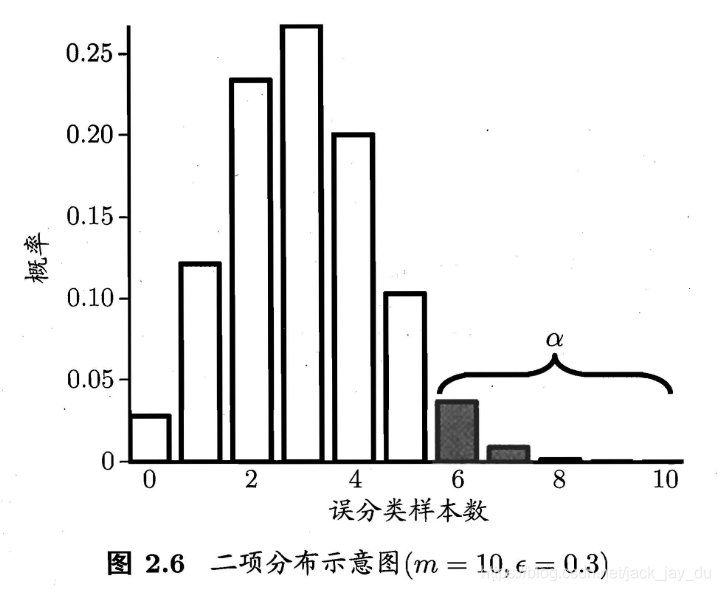
$\alpha$ 的常用取值有0.05, 0.1

这里 $1-\alpha$ 反映了结论的"置信度"(confidence),直观来看, 即非阴影部分的面积

\bar{\epsilon} = min \epsilon \space s.t. \space \sum\limits^m_{i = \epsilon \times m + 1} \begin{pmatrix} m \\ i \end{pmatrix}\epsilon^i_0(1 - \epsilon_0)^{m-i} < \alpha

通过多次重复留出法或是交叉验证法等进行多次训练/测试, 这样会得到多个测试错误率, 此时可使用"t检验"(t-test). 假定我们得到了一个k个测试错误率, $\hat{\epsilon}_1, \hat{\epsilon}_2, ..., \hat{\epsilon}_k$ , 则平均测试错误率 $\mu$ 和方差 $\sigma^2$ 为

\mu = \frac{1}{k}\sum\limits^k_{i=1}\hat{\epsilon}_i

\sigma^2 = \frac{1}{k - 1}\sum\limits^k_{i=1}(\hat{\epsilon}_i-\mu)^2

考虑到这k个测试错误率可看作泛化错误率$$\epsilon_0$$的独立采样, 则变量

\tau_t = \frac{\sqrt{k}(\mu - \epsilon_0)}{\sigma}

$\alpha$	k = 2	k = 5	k = 10	k = 20	k = 30
0.05	12.706	2.776	2.262	2.093	2.045
0.10	6.314	2.132	1.833	1.729	1.699

2.4.2 交叉验证t检验

对两个学习器A和B, 若我们使用k折交叉验证法得到的测试错误率分别为 $\epsilon^A_1, \epsilon^A_2, ..., \epsilon^A_k$ 和 $\epsilon^B_1, \epsilon^B_2, ..., \epsilon^B_k$ , 其中 $\epsilon^A_i$ 和 $\epsilon^B_i$ 是在相同的第i折训练/测试集上得到的结果, 则可用k折交叉验证"成对t检验"(paired t-tests)来进行比较检验

这里的基本思想是若两个学习器的性能相同, 则它们使用相同的训练/测试集得到的测试错误率应相同, 即 $\epsilon^A_i = \epsilon^B_i$

具体来说, 对k折交叉验证产生的k对测试错误率:

先对每对结果球差, $\Delta_i = \epsilon^A_i - \epsilon^B_i$
若两个学习器性能相同, 则差值均值应为0.
因此, 可根据差值, 来对学习器A与B性能相同这个假设做t检验, 计算出差值的均值 $\mu$ 和方差 $\sigma^2$ , 在显著度 $\alpha$ 下,若变量
$\tau_t = \vert\frac{\sqrt{k}\mu}{\sigma}\vert$
小于临界值 $t_{\alpha/2, k-1}$ , 则假设不能被拒绝, 即认为两个学习器的性能没有显著差别
否则可认为两个学习器的性能有显著差别, 且平均错误率较小的那个学习器性能较优

因为样本有限, 在使用交叉验证等实验估计法时, 不同轮次的训练集会有一定的重叠, 为缓解这个问题可以使用"5x2交叉验证"

2.4.3 McNemar检验

对于二分问题, 使用留出法不仅可估计出学习器A和B的测试错误率, 还可获得两学习器分类结果的差别, 即两者都正确、都错误、一个正确一个错误的样本数:

算法B	算法A: 正确	算法A: 错误
正确	$e_{00}$	$e_{01}$
错误	$e_{10}$	$e_{11}$

若我们做的假设是两学习器性能相同, 则应有 $e_{01} = e_{10}$ , 那么变量 $|e_{01} - e_{10}|$ 应当服从正态分布. McNemar检验考虑变量

\tau_{X^2} = \frac{(|e_{01} - e_{10}| - 1)^2}{e_{01} + e_{10}}

服从自由度为1的 $X^2$ 分布, 即标准正态分布变量的平方.

当以上变量值小于临界值 $X^2_\alpha$ 时, 不能拒绝假设, 即认为两学习器的性能没有显著差别
否则拒绝假设, 即认为两学习器性能有显著差别, 且平均错误率较小的那个学习器性能较优

2.4.4 Friedman检验与Nemenyi后续检验

数据集	算法A	算法B	算法C
$D_1$	1	2	3
$D_2$	1	2.5	2.5
$D_3$	1	2	3
$D_4$	1	2	3
平均序值	1	2.125	2.875

使用Friedman检验来判断这些算法是否性能相同.若相同, 则他们的平均序列应当相同.假定我们在N个数据集上比较k个算法, 令 $r_i$ 表示第i个算法的平均序值, (不考虑平分序值)则 $r_i$ 的均值和方差分别为 $(k+1)/2$ 和 $(k^2-1)/12N$ . 变量

\tau_{X^2} = \frac{k -1}{k}·\frac{12N}{k^2 - 1} \sum\limits^k_{i = 1}(r_i - \frac{k + 1}{2})^2

=\frac{12N}{k(k+1)}(\sum\limits^k_{i=1}r_i^2-\frac{k(k+1)^2}{4})

在k和N都较大时, 服从自由度为k-1的 $X^2$ 分布

然而上述的圆石Friedman检验过于保守, 现在通常使用变量

\tau_F = \frac{(N - 1)\tau_{X^2}}{N(k - 1) - \tau_{X^2}}

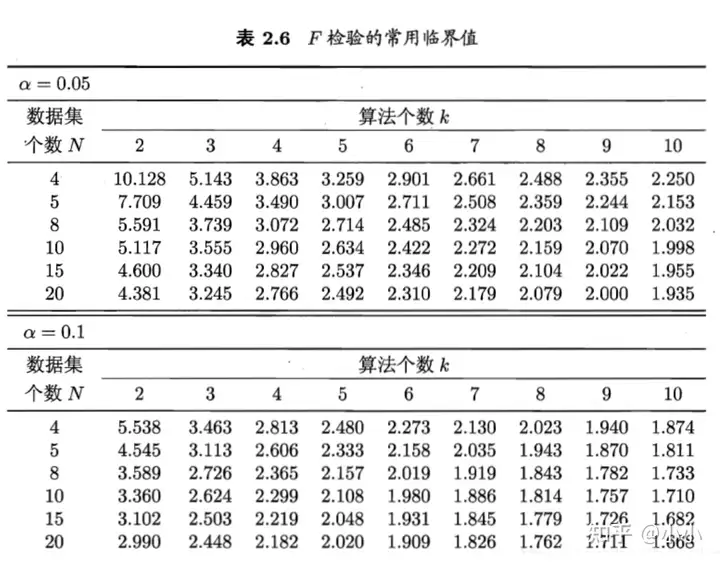
若"所有算法的性能相同"这个假设被拒绝, 则说明算法的性能显著不同.这时需进行"后续检验"(post-hoc test)来进一步区分个算法. 常用的有Nemenyi后续检验.

Nemenyi检验计算出平均序值差别的临界值域

CD = q_\alpha\sqrt{\frac{k(k+1)}{6N}}

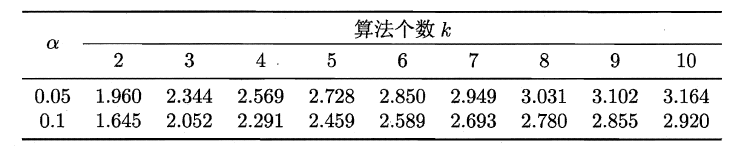
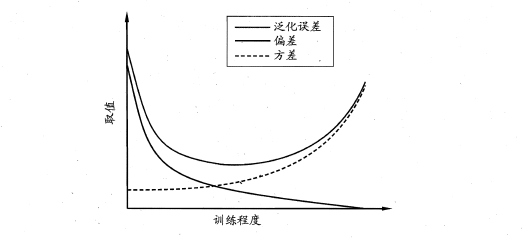
2.5 偏方与方差

在回归任务中

学习算法的期望预测:

\bar{f}(x) = E_D[f(x;D)]

使用样本数相同的不同训练集产生的方差为:

var(x) = E_D[(f(x;D)-\bar{f}(x))^2]

噪声为:

\varepsilon^2 = E_D[(y_D - y)^2]

期望输出与真是标记的差别成为偏差(bias), 即:

bias^2(x) = (\bar{f}(x)-y)^2

泛化误差可分解为偏差、方差、与噪声之和

E(f;D) = bias^2(x) + var(x) + \varepsilon^2

3. 线性模型

3.1 基本形式

给定有d个属性描述的实例 $\vec{x} = (x_1;x_2;...;x_d)$ , 其中 $x_i$ 是x在第i个属性上的取值, 线性模型(linear model)试图学得一个通过属性的线性组合来进行预测的函数, 即

f(\vec{x}) = w_1x_1 + w_2x_2 + ... + w_dx_d + b，

一般用向量形式写成

f(\vec{x}) = \vec{w}^T\vec{x} + b

3.2 线性回归

给定数据集 $D = {(x_1, y_1), (x_2, y_2),...,(x_m,y_m)}$ , 其中 $x_i = (x_{i1};x_{i2};...;x_{id}), y_i \in R$

线性回归试图学得

f(x_i) = wx_i + b, 使得f(x_i)\simeq y_i

均方误差最小化:

(w^*, b^*) = \arg min\sum\limits^m_{i=1}(f(x_i) - y_i)^2

= \arg min \sum\limits^m_{i=1}(y_i - wx_i - b)^2

$w^*, b^*$ 表示 $w$ 和 $b$ 的解

均方误差有非常好的几何意义, 它对应了常用的欧几里得距离或简称"欧式距离"(Euclidean distance). 基于均方误差最小化来进行模型求解的方法成为"最小二乘法"(least square method).

求解 $w$ 和 $b$ 使 $E_{(w,b)} = \sum^m_{i=1}(y_i - wx_i- b)^2$ 最小化的过程, 称为线性回归模型的最小二乘"参数估计"(parameter estimation). 我们可将 $E_{(w,b)}$ 分别对 $w$ 和 $b$ 求导, 得到

\frac{\partial E_{w,b}}{\partial E_w} = 2 (w\sum\limits^m_{i=1}x_i^2 - \sum\limits^m_{i = 1}(y_i - b)x_i)

\frac{\partial E_{w,b}}{\partial E_w} = 2 (mb - \sum\limits^m_{i = 1}(y_i - wx_i))

然后令上两式为0, 可得到$w$和$b$最优解的闭式(closed-form)解

w = \frac{\sum\limits^m_{i=1}y_i(x_i - \bar{x})}{\sum\limits^m_{i = 1}x^2_i - \frac{1}{m}(\sum\limits^m_{i = 1}x_i)^2}

b = \frac{1}{m}\sum\limits^m_{i = 1}(y_i - wx_i)

其中 $\bar{x} = \frac{1}{m}\sum\limits^m_{i = 1}x_i$ 为 $x$ 的均值

更一般的形式为:

f(\vec{x}_i) = \vec{w}_T\vec{x}_i + b, 使得f(\vec{x}_i)\simeq y_i

这称为"多元线性回归"(multivariate linear regression)

可利用最小二乘法来对 $\vec{w}$ 和 $b$ 进行估计. 为便于讨论, 我们把 $\vec{w}$ 和 $b$ 吸收入向量形式 $\hat{\vec{w}}=(\vec{w};b)$ , 相应的, 把数据集D表示为一个 $m\times(d+1)$ 大小的矩阵 $\vec{X}$ ,其中每行对应于一个示例, 该行前 $d$ 个元素及对应于实例的 $d$ 个属性值, 最后一个元素恒置为1, 即

\vec{X} = \begin{pmatrix} x_{11} & x_{12} & ... & x_{1d} & 1 \\ x_{21} & x_{22} & ... & x_{2d} & 1 \\ ... & ... & ... & ... & ... \\ x_{m1} & x_{m2} & ... & x_{md} & 1 \end{pmatrix} = \begin{pmatrix} \vec{x}^T_1 & 1 \\ \vec{x}^T_2 & 1 \\ ... & ... \\ \vec{x}^T_m & 1 \end{pmatrix}

再把标记也写成向量形式 $\vec{y} = (y_1;y_2;...;y_m)$ , 有

\hat{\vec{w}}^* = \arg\limits_{\hat{\vec{w}}}\min(\vec{y} -\vec{X}\hat{\vec{w}})^T(\vec{y} - \vec{X}\hat{\vec{w}})

令 $E_{\hat{\vec{w}}} = (\vec{y} -\vec{X}\hat{\vec{w}})^T(\vec{y} - \vec{X}\hat{\vec{w}})$ , 对 $\hat{\vec{w}}$ 求导得到

\frac{\partial E_{\hat{\vec{w}}}}{\partial\hat{\vec{w}}} = 2 \vec{X}^T(\vec{X}\hat{\vec{w}} - \vec{y})

当 $X^TX$ 为满秩矩阵(full-rank matrix)或正定矩阵(positive definite matrix)时, 上式为零可得

\hat{\vec{w}}^* = (\vec{X}^T\vec{X})^{-1}\vec{X}^T\vec{y}

其中 $(\vec{X}^T\vec{X})^{-1}$ 是矩阵 $(\vec{X}^T\vec{X})$ 的逆矩阵. 令 $\hat{\vec{x}}_i = (\vec{x}_i,1)$ ,则最终学得的多元线性回归模型为

f(\hat{x}_i) = \hat{x}^T_i(X^TX)^{-1}X^Ty

假设我们认为示例所对应的输出标记是在指数尺度上变化, 那就可将输出标记的对数作为线性模型逼近的目标, 即
$\ln y = \vec{w}^T\vec{x} + b$
这就是"对数线性回归"(log-linear regression), 它实际上是在试图让 $e^{\vec{w}^T\vec{x}+b}$ 逼近 $y$ .
其作用是把一个非线性关系通过对数形式转换成线性关系
更一般的，考虑单调可微函数 $g(·)$ , 令
$y = g^{-1}(\vec{w}^T\vec{x}+b)$
这样得到的模型成为"广义线性模型"(generalized linear model)，其中函数 $g(·)$ 称为"联系函数"(link function).通过联系函数把非线性关系转换成线性关系， $\ln(·)$ 就是其中一种

3.3 对数几率回归(逻辑回归)

线性回归产生的预测值:

Z = \vec{w}^T\vec{x}+b

对数几率函数(logistic function):

y = \frac{1}{1 + e^{-z}}\\ \ln\frac{y}{1-y} = \vec{w}^T\vec{x}+b

对数几率函数(逻辑回归函数)通过函数把需要分类的值(这里指二元分类)压缩成一个连续的阶跃函数

几率(odds):

\frac{y}{1-y}

对数几率(logit):

\ln\frac{y}{1-y}

通过以上式子可得:

p(y = 1|x) = \frac{e^{\vec{w}^T\vec{x}+b}}{1+e^{\vec{w}^T\vec{x}+b}} \\ p(y = 0|x) = \frac{1}{1+e^{\vec{w}^T\vec{x}+b}}

可通过"极大似然法"(maximum likelihood method)来估计 $w$ 和 $b$ . 给定数据集 $\{(\vec{x}_i,y_i)\}^m_{i = 1}$ , 对率回归模型最大化"对数似然"(log-likelihood)

\ell(\vec{w}, b) = \sum\limits^m_{i=1}\ln p(y_i|\vec{x}_il;\vec{w},b)\\

即令每个样本属于其真实标记的概率越大越好.

为便于讨论
令 $\beta = (\vec{w};b)$ , $\hat{\vec{x}} = (\vec{x};1)$
即
$p(y_i|\vec{x}_i;\vec{w}, b) = y_ip_1(\hat{\vec{x}}_i; \beta) + (1 - y_i) p_0 (\hat{\vec{x}}_i; \beta)$

结合上式，并最大化可获得:

\ell(\beta) = \sum^m_{i=1}(-y_i\beta^T\hat{\vec{x}}_i+ \ln(1+e^{\beta^T\hat{\vec{x}}_i}))

根据凸优化理论，利用优化算法可得:

\beta^* = \argmin\limits_\beta l(\beta)

以牛顿法为例:

\beta' = \beta - (\frac{\partial^2\ell(\beta)}{\partial\beta\partial\beta^T})^{-1}\frac{\partial \ell(\beta)}{\partial\beta}\\ \frac{\partial\ell(\beta)}{\partial\beta} = - \sum^m_{i = 1} \hat{\vec{x}_i}(y_i - p_1(\hat{\vec{x}_i; \beta}))\\ \frac{\partial^2\ell(\beta)}{\partial\beta\partial\beta^T} = \sum^m_{i=1}\hat{\vec{x}}_i\hat{\vec{x}}_i^Tp_1(\hat{\vec{x}}_i; \beta)(1 - p_1(\hat{\vec{x}}_i; \beta))

3.4 线性判别分析

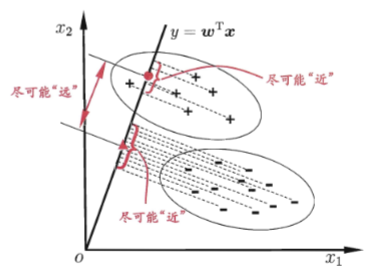
欲使同样样例的投影点尽可能接近，可以让同类样例投影点的协方差尽可能小，即 $\vec{w}^T\sum_0\vec{w} + \vec{w}^T\sum_1\vec{w}$ 尽可能小

欲使异类样例的投影点尽可能远离，可以让类中心之间的距离尽可能大，即 $||\vec{w}^T\mu_0 - \vec{w}^T\mu_1||^2_2$ 尽可能小

\begin{aligned}\text{J}&=\frac{\|\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_0-\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_1\|_2^2}{\boldsymbol{w}^\mathrm{T}\boldsymbol{\Sigma}_0\boldsymbol{w}+\boldsymbol{w}^\mathrm{T}\boldsymbol{\Sigma}_1\boldsymbol{w}}\\&=\frac{\boldsymbol{w}^\mathrm{T}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^\mathrm{T}\boldsymbol{w}}{\boldsymbol{w}^\mathrm{T}(\boldsymbol{\Sigma}_0+\boldsymbol{\Sigma}_1)\boldsymbol{w}} .\end{aligned}

定义“类内散度矩阵”(within-class scatter matrix)

\begin{aligned} \mathbf{s}_{w}& =\boldsymbol{\Sigma}_0+\boldsymbol{\Sigma}_1 \\ &=\sum_{x\in X_{0}}\left(\boldsymbol{x}-\boldsymbol{\mu}_{0}\right)\left(\boldsymbol{x}-\boldsymbol{\mu}_{0}\right)^{\mathrm{T}}+\sum_{x\in X_{1}}\left(\boldsymbol{x}-\boldsymbol{\mu}_{1}\right)\left(\boldsymbol{x}-\boldsymbol{\mu}_{1}\right)^{\mathrm{T}} \end{aligned}

参考书籍: 《机器学习》- 周志华著

机器学习:笔记 - Machine Learning Note

阅读此文章之前，你可能需要首先阅读以下的文章才能更好的理解上下文。

机器学习:笔记 - Machine Learning Note

2. 模型评估与选择

2.1 经验误差与过拟合

2.2 评估方法

2.2.1 留出法

2.2.2 交叉验证法

2.2.3 自助法

2.2.4 调参和最终模型

2.3 性能度量

2.3.1 错误率与精度

2.3.2 查准率、查全率与F1

2.3.3 ROC与AUC

2.3.4 代价敏感错误率与代价曲线

2.4 比较检验

2.4.1 假设验证(hypothesis test)

2.4.2 交叉验证t检验

2.4.3 McNemar检验

2.4.4 Friedman检验与Nemenyi后续检验

2.5 偏方与方差

3. 线性模型

3.1 基本形式

3.2 线性回归

3.3 对数几率回归(逻辑回归)

3.4 线性判别分析